저의 근본없는 러프한 지식으로 말하자면 ADT는 결국 product type 과 sum type 을 제공한다는 의미입니다. 그런데 product type은 모던한 언어든 아니든 실용적으로 사용되는 언어는 결국 다 제공하는 셈이라서, 어떤 언어가 ADT를 제공하는가라는 문제는 사실상 어떤 언어가 sum type을 제공하는가라는 문제와 거의 같은 문제가 됩니다.
product type은 결국 (타입이 정해진) tuple이나 record 타입입니다. 이들이 cartesian product와 유사하다는 의미에서 product type 이라는 명칭을 가지고 있습니다. 어떤 키와 타입이 대응되는 합성된 타입이죠. 다음의 예를 봅시다.
- (int, string, double)
- {age:int, name:string, weight:double}
(17, 김바보, 67.0), (21, 박천재, 55.0)은 모두 1에 속합니다. 그리고 index가 0이면 int형일 것이고, index가 1이면 string, index가 2이면 double형입니다. 튜플의 인덱스와 타입이 대응되서 정해져 있죠.
{age:17, name:김바보, weight:67.0}, {age:21, name:박천재, weight:55.0} 역시 age, name, weight라는 키에 따라서 정해진 타입이 정해져 있습니다.
C/C++/C#의 struct, C++/JAVA/C#의 클래스 등등 딱히 모던하다는 평을 받지 않는 언어로 프로그래밍을 할 때에도 product type을 활용하는 것은 어렵지 않습니다.
문제는 sum type입니다. 제대로 된 sum type을 지원하지 않는 언어가 많았고, 지금도 저는 어떤 언어들이 sum type을 지원하는 방식은 마음에 들지 않습니다.
그러면 어떤 sum이냐? 디지털을 다루는 사람들에게, 어떤 경우에 sum은 or를 의미하죠. sum type도 마찬가지입니다. SumTypeA 가 Type1 + Type2 라면, 타입이 SumTypeA인 변수는 Type1, Type2 둘 중의 하나가 될 수 있습니다.
한편 sum type 을 지원하는 언어는 거의 반드시 타입 스위치에 해당하는 기능을 함께 제공됩니다. 예를 들면 switch-case 문에서 SumTypeA 변수의 타입으로 case를 나눈다면 Type1과 Type2인 경우를 모두 처리하도록 강제하는 식입니다.
한편 이 글을 읽기 전 sum type을 모르던 분이 여기까지 읽고 enum 타입을 떠올리셨다면 올바른 방향을 잡으신 겁니다. enum은 sum type의 특수한 형태죠. 그럼 더 일반적인(general한) sum type은 무엇을 할 수 있느냐? 이진트리구조를 다음과 같이 나타낼 수 있습니다.
type Tree =
| Leaf
| Node of value: int * left: Tree * right: Tree
let tree = Node(5, Node(1, Leaf, Leaf), Node(3, Leaf, Node(4, Leaf, Leaf)))
F#은 모릅니다만 Node (int, Tree, Tree) 를 최상단으로 놓고 시작해서 Tree 자리에 Node (int, Tree, Tree) 와 Leaf 중에 하나를 택해 치환하는 방식으로 확장되었다는 점은 알아볼 수 있겠습니다. 위의 F# 코드는 아래의 트리를 묘사하는 것이지요.
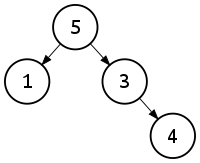
그럼 sum type이 없을 때와 비교해서 위의 코드가 무엇이 나은가?
자바로 같은 일을 하는 코드를 짠다면 Tree라는 자료구조를 보여주는 타입은 등장하지 않는 경우가 보통일 겁니다. (저는 사실 그렇게 할 수 있는 방법을 잘 모르겠습니다.) Tree라는 이름을 클래스 이름으로 쓸 수는 있는데, 실제로 그 클래스가 나타내는 것은 트리가 아니라 노드일 겁니다.
자바에서 노드가 트리가 되는 과정은 타입 자체에 나타나지 않습니다. 따로 자료구조를 공부하거나, 아니면 예제코드를 보면서 이해해야 합니다. 그런데 그 예제코드는 어떤 형태일까요?
위의 F# 코드는 declarative합니다. 타입 선언이니까요. 그리고 recursive한 타입이죠. 위의 재귀적 타입을 expand 하는 것은 훈련되지 않았을 때 쉽기만 한 일은 아닙니다만, 그 문턱을 넘을 수 있다면 타입 자체에 자료형이 이미 설명되어 있습니다.
그러나 자바 코드라면 operation일 겁니다. right와 left에 null이나 아니면 다른 노드를 assign하는 '동작'이 들어갑니다. 그 과정을 머리로 굴리면서 이해해야 하는 것이죠.
BNF로 정의된 문법의 파서를 만드는 경우라면 어떨까요? sum type은 abstract syntax를 만드는 데 큰 도움이 된다고 합니다. BNF의 | 기호를 처리하기에 sum type만한 것이 있을 것 같지는 않군요. 아래는 하스켈 코드라고 합니다.
data Expression = Number Int
| Add Expression Expression
| Minus Expression Expression
| Mult Expression Expression
| Divide Expression Expression
모든 경우의 수를 처리했는지 여부를 컴파일러가 도와주므로, AST를 처리하는 과정 역시 비지터 패턴 코드보다 훨씬 즐거울 겁니다.
자바에서 노드가 트리가 되는 과정은 타입 자체에 나타나지 않습니다. 따로 자료구조를 공부하거나, 아니면 예제코드를 보면서 이해해야 합니다. 그런데 그 예제코드는 어떤 형태일까요?
위의 F# 코드는 declarative합니다. 타입 선언이니까요. 그리고 recursive한 타입이죠. 위의 재귀적 타입을 expand 하는 것은 훈련되지 않았을 때 쉽기만 한 일은 아닙니다만, 그 문턱을 넘을 수 있다면 타입 자체에 자료형이 이미 설명되어 있습니다.
그러나 자바 코드라면 operation일 겁니다. right와 left에 null이나 아니면 다른 노드를 assign하는 '동작'이 들어갑니다. 그 과정을 머리로 굴리면서 이해해야 하는 것이죠.
BNF로 정의된 문법의 파서를 만드는 경우라면 어떨까요? sum type은 abstract syntax를 만드는 데 큰 도움이 된다고 합니다. BNF의 | 기호를 처리하기에 sum type만한 것이 있을 것 같지는 않군요. 아래는 하스켈 코드라고 합니다.
data Expression = Number Int
| Add Expression Expression
| Minus Expression Expression
| Mult Expression Expression
| Divide Expression Expression
모든 경우의 수를 처리했는지 여부를 컴파일러가 도와주므로, AST를 처리하는 과정 역시 비지터 패턴 코드보다 훨씬 즐거울 겁니다.
다만 저는 kotlin과 scala의 sealed type 형태로 구현된 sum type은 좋아하지 않습니다. 이 두 언어의 sum type은 결국 A는 A1 또는 A2라는 관계를 상속을 통한 polymorphism으로 처리합니다. 원래의 sum type에는 없었던, 공동의 부모를 가져야 한다는 불필요한 제약이 생기는 거죠. :-/ sum type의 제한된 형태인 enum을 확장시키는 방향으로 접근해서 생기는 한계가 아닐까 싶은데 그런 식으로 구현한 이유는 잘 모르겠습니다. JVM의 한계일까요? :-(
댓글 없음:
댓글 쓰기